内容预览
全文总字数:1527字
【一笔画难题的数学革命】在人类智慧的长河中,有一个看似简单却困扰了无数人的经典问题:如何一次性不重复地通过所有桥梁并返回原点?这不仅是18世纪哥尼斯堡居民茶余饭后的消遣话题,更是一个引发数学革命的思维起点。它从具体的地理现象逐渐升华为抽象的数学难题,最终催生了图论与几何拓扑学的新分支,彻底改变了人类对空间结构的认知方式。
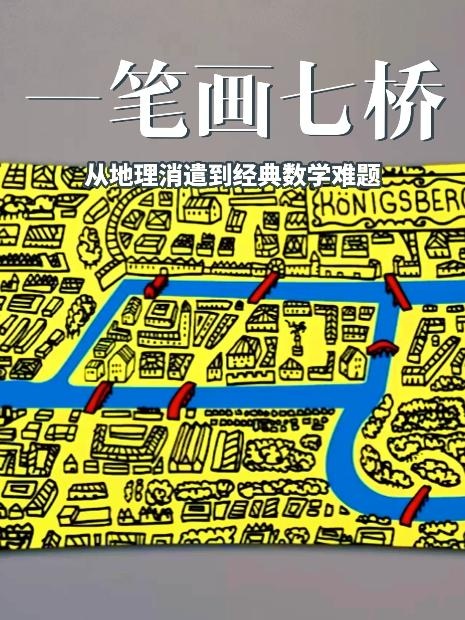
故事起源于普雷格尔河畔的哥尼斯堡城。这座城市的独特地理布局构成了难题的物理基础——河中心的两座岛屿与两岸陆地通过七座桥梁相互连接。当地居民时常在散步时思考:能否从任意一块陆地出发,恰好经过每座桥一次,最终回到起点?尽管这个问题听起来像是简单的游戏,但在相当长的时间里,竟无人能找到实现路径。随着讨论热度的持续发酵,这个问题逐渐传到了学术界。一些大学生将难题写信告知了著名数学家欧拉,期待他能破解这个令人困惑的谜题。
起初欧拉认为这个问题缺乏数学意义,但当他尝试用传统几何方法求解时,却发现现有的数学工具根本无法应对这个看似简单的问题。这种认知落差激发了他的研究热情。经过数年探索,欧拉在1736年向圣彼得堡科学院提交了关于哥尼斯堡七桥问题的论文。在这篇划时代的著作中,他创造性地将实际问题转化为抽象数学模型:把四块陆地抽象为四个点,七座桥梁则表示为连接这些点的线。这种转换使问题从具体的地理问题升华为数学上的"一笔画"问题——能否用笔不离纸的方式连续画出整个图形,且每条边只经过一次?
欧拉通过严密的逻辑推理证明:哥尼斯堡七桥问题根本无解。这一结论震惊了当时的数学界。更重要的是,他从中归纳出了具有普遍意义的一笔画定理,即后世所称的欧拉定理。该定理明确指出:当图形中....全文更精彩